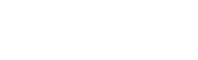Some mXmas fun

With the holidays approaching we thought we would send everyone some mXmas presents! And obviously what everyone wants for mXmas are mXrap videos ?. These videos are not geotech related but come from various games, generative art, or physics simulations that we have made for fun. Scroll down for more details. The mXrap team wishes […]
Energy – moment relationship
Energy and moment are two independent measures of the strength of a seismic event. Their physical meaning and how they are calculated was described in a previous blog post. Analysis of the relationship between the energy and moment of events can provide insight into seismic sources. For example, blasts or ore pass noise, falsely processed […]
mXsync updates

For users who have upgraded to mXrap version 5.16+, you may have noticed the new mXsync button at the bottom left of all of the windows. This button allows users to open mXsync from within mXrap to apply patches and complete backups of the root folder. When this button is blinking, it signifies that you […]
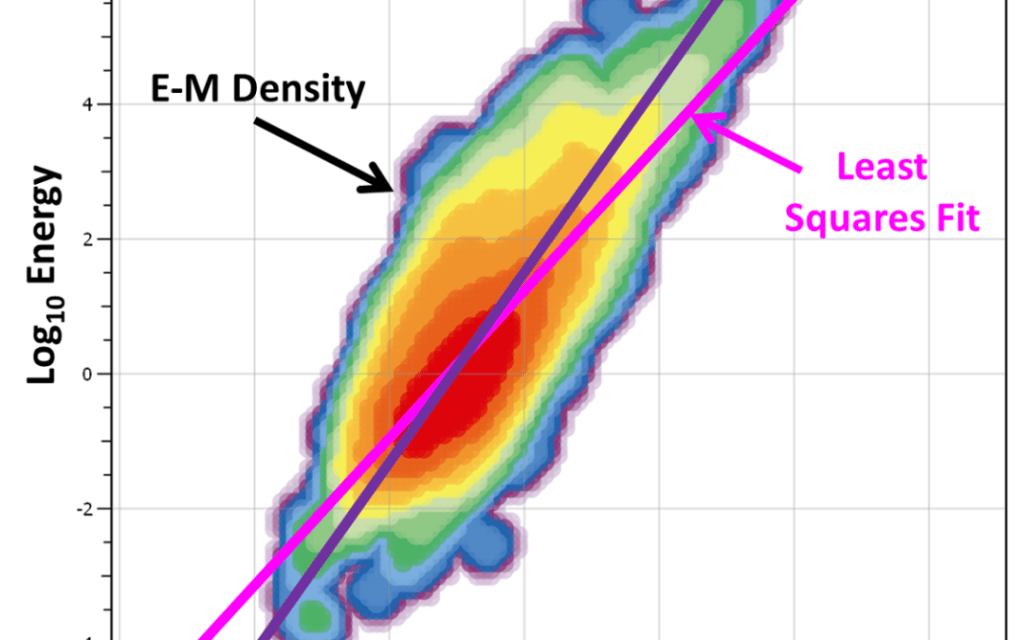
Caving Suite updates
The Caving Suite is a set of applications that provide tools for the analysis and interpretation of cave monitoring data sources. Currently, four apps are included in the Caving Suite: Caving Sandbox, Fragmentation, Open Hole Dipping, and Caving Hydraulic Radius (see app overview for more details) Over the past year, there has be numerous updates to […]
Rock Mass Data Analyser updates

The Rock Mass Data Analyser (RMDA) application allows a user to import various types of geotechnical data (rock mass quality, structural, stress and intact rock strength) into mXrap, creating a geotechnical database which may be visualised and analysed in 3D, on charts and in stereonets (see previous blog post for more details). Since the release […]
Reset variables and filters

Have you ever been using mXrap and wanted to reset your filters or reset all your variables to the defaults? We have a button for that! Simply open up the workspaces menu in the top left of the Viewer window, then press the ‘Reset Variables to Defaults’. This should reset all variables, resetting all filters […]
New tool – Datamine file converter

If you use Datamine at your site, we now have a tool to help you batch convert the datamine TR and PT files into mXrap-readable dxf files. To get access to this tool, please contact the support email address at our support email address.
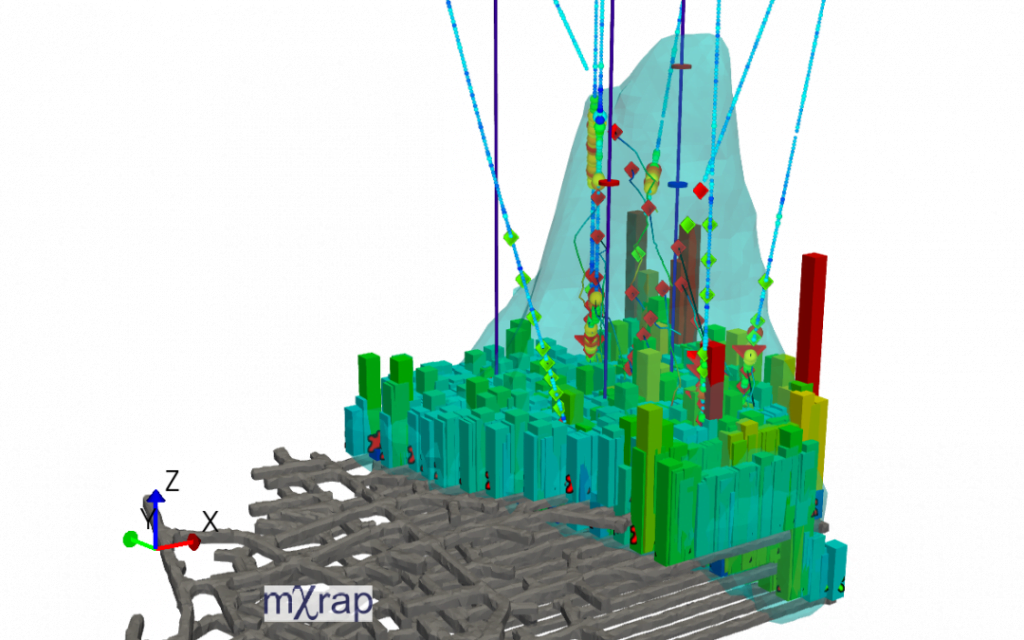
Update to Paste Backfill Design app

We have made a couple of changes to the Paste Backfill Design application since the original release. See the previous blog post for the main details of the app. Since the first release, we have modified the paste volume calculations to allow for multiple pouring locations and beach angles. This will be helpful for cases […]
NEW APP – Paste Backfill Design
We have developed a new app to aid in the design of paste backfill in stoping operations. The app has tools to help you to: If you would like to try out the app, please contact our info email. Paste volumes The paste volume calculations use the mine geometry app to input surveyed geometry. Walls/barricades […]