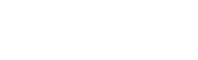Energy – moment relationship
Energy and moment are two independent measures of the strength of a seismic event. Their physical meaning and how they are calculated was described in a previous blog post. Analysis of the relationship between the energy and moment of events can provide insight into seismic sources. For example, blasts or ore pass noise, falsely processed […]
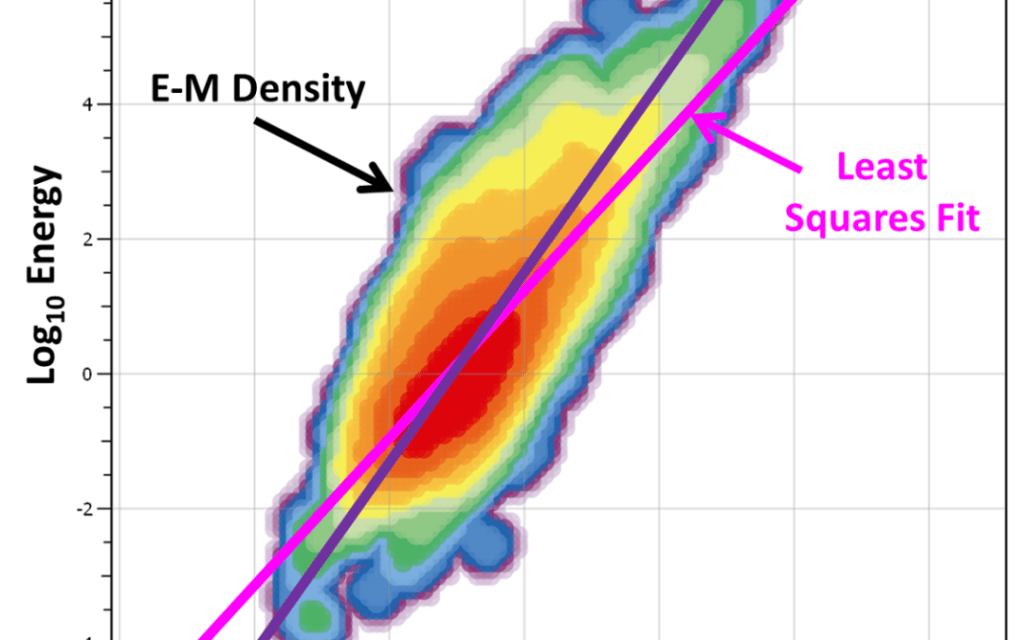
Plane based analysis
The Grid Based Analysis now has a plane based function. The user can select a plane (defined in the plane editor window) and display cumulative or average parameters on that plane. Like the grid, the average and cumulative parameters are calculated differently. For the average parameters, the plane points are treated identically to the grid […]
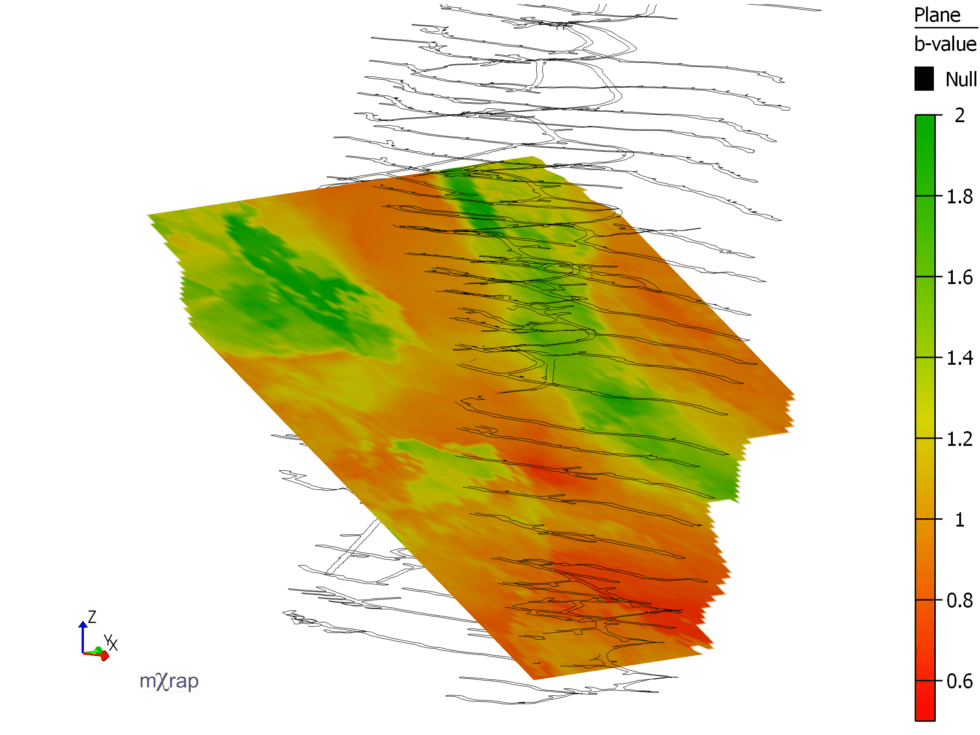
Seismic source parameters – quick guide
As mentioned in the last blog post, energy and moment are independently calculated based on the displacement and velocity spectra of the recorded waveforms. Another spectral parameter is the corner frequency. The figure on the left shows the corner frequency (f0) on theoretical displacement, velocity and acceleration spectra. The calculation of corner frequency relies on […]
Seismic energy and moment

You know that energy and moment are parameters to describe seismic events. But what exactly is their physical meaning for a seismic event source and how are they calculated? Moment and energy are both separate (but related) measures of the strength of a seismic event. A similar example is a car engine, the performance is […]