Grids

Grids are a dynamic tool used throughout mXrap to form seismic populations, perform calculations and display results. Taking time to set-up site appropriate grids not only makes performing analysis in mXrap more efficient, but it enables others to easily replicate your results. Most sites benefit from a mine and/or orebody wide coarse (sparse) and relatively dense grid, plus additional higher resolution (dense) grids for areas of interest.
Hazard Assessment – Event Rate

The Hazard Assessment application uses a grid-based approach to describe the seismic hazard throughout your mine. Each grid point essentially represents a seismic source with a specific frequency-magnitude relationship. A frequency-magnitude relationship is defined from the MUL, Mmin, b-value, and event rate. The event rate is something we haven’t taken a dive into yet, so we’ll get into it in this post. Event rate sounds like a simple calculation but there are quite a few complexities worth explaining.
Sensitivity Analysis in Hazard Assessment app

A new window has been added to the Hazard Assessment app (Figure 1). The sensitivity analysis aims to quantify the effect of the variation of the input parameters on the hazard. These analyses can also help the user to determine the optimal settings to use for many of the parameters. This window allows the user […]
Updates to Hazard Assessment app
A few new features have been added to the Hazard Assessment application, aiming to improve usability, understanding and investigation. The first addition is a chart in the hazard setup window to indicate the current date range settings. Usually the date range for calculating b-value will be a lot longer than for calculating event rate. Hopefully […]
Background filters in the hazard app
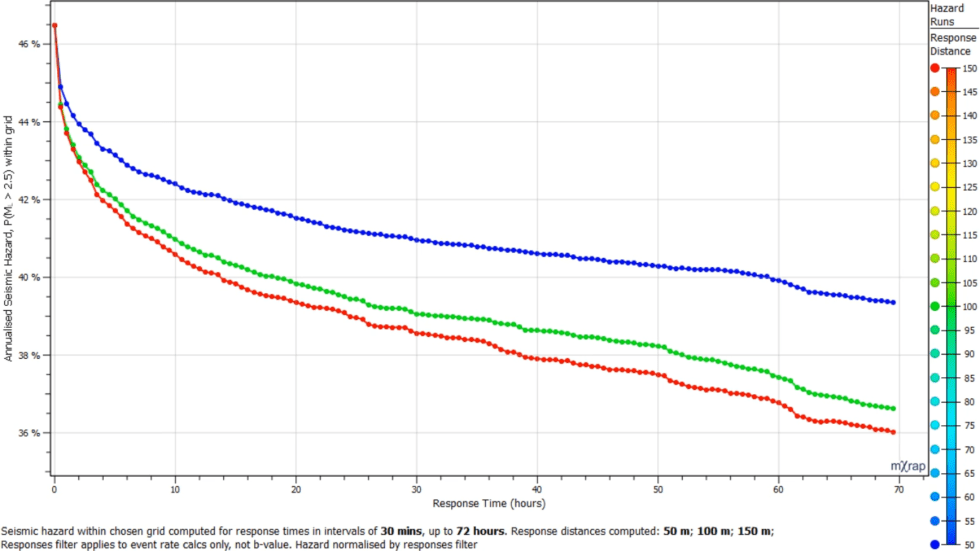
The new background filters have been added to the Hazard Assessment application. The time of day filter can be used to see the effect of removing events during blasting/shift change on the hazard results. You can either view the results in raw or normalised form. The hazard calculations do normalisation for the event rate calcs […]
Stochastic declustering explained
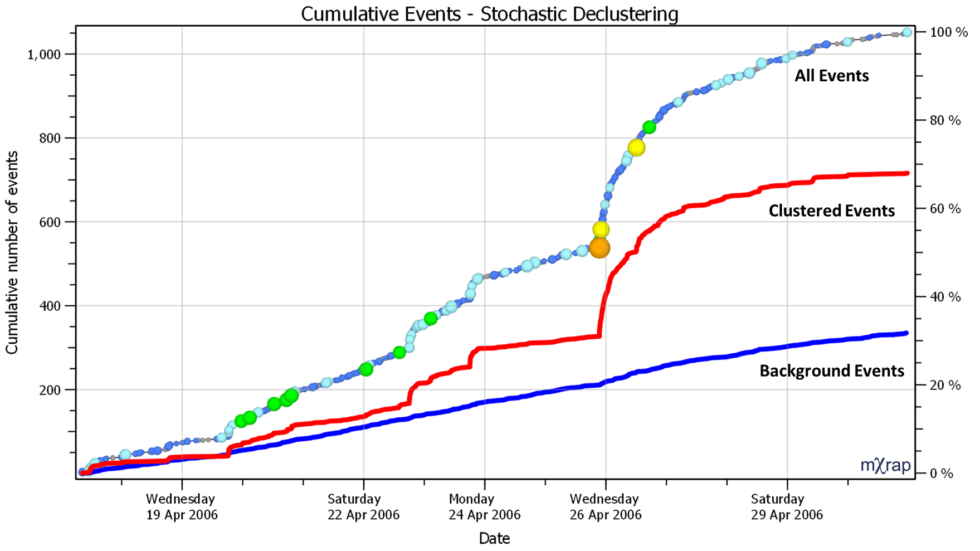
As mentioned in the last blog post, a stochastic declustering algorithm has been implemented in mXrap to separate events into ‘clustered’ and ‘background’ components. It can be useful when designing seismic exclusions and re-entry procedures to separate seismicity that occurs in short bursts from seismicity that has low variability in space and time. Short-term exclusions […]
New b-value isosurfaces
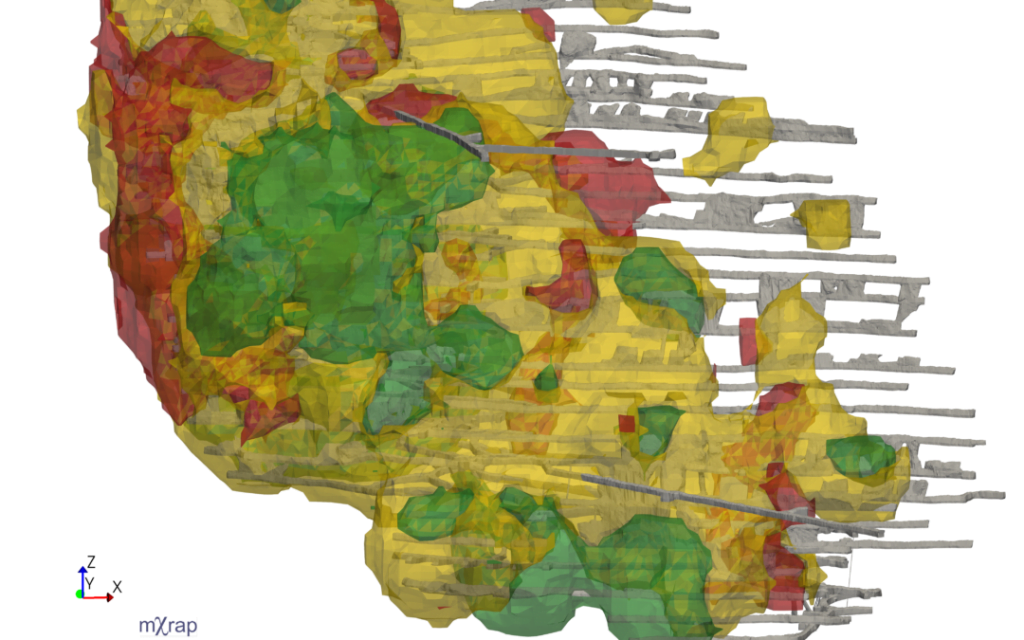
The isosurfaces for b-value have been upgraded in the latest root. There is now much more control over the isosurface levels. Up to 5 iso’s can be plotted for user defined ranges. A linguistic name can be assigned to each level and displayed in the legend. A new video has been uploaded to the Hazard […]
Hazard Assessment app – excavation view

The grid-based hazard calculations in the Hazard Assessment app were discussed in a previous post. The Iso View describes the hazard at all locations within the mine but when you are considering the seismic risk for a particular work area, large events and strong ground motions may come from multiple sources. The Excavation View estimates […]
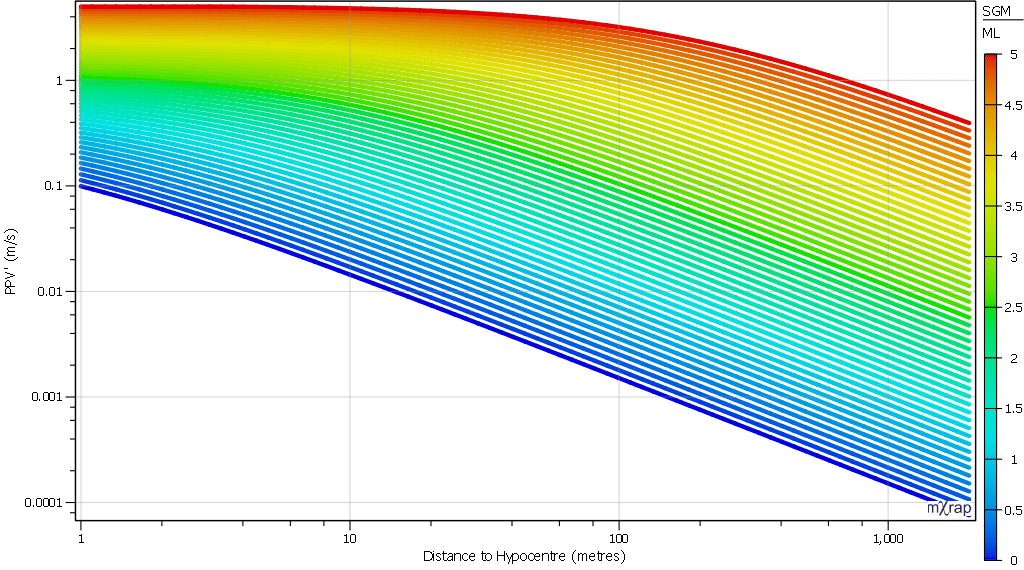
Strong ground motion relationship

The strong ground motion (SGM) relationship is used to calculate the peak particle velocity (PPV) generated by a seismic event. You may also hear this referred to as a ground motion prediction equation (GMPE), but only the maximum velocity is estimated, i.e. the strong ground motion, rather than the full, complex wave motion. The PPV […]
What do the hazard iso’s mean?

The Iso View in the Hazard Assessment application expresses the seismic hazard in two ways. The current yearly hazard within the chosen grid volume. This is shown in the footer of the 3D view, as the probability of an event exceeding the design magnitude. The spatial distribution of the hazard. This is highlighted by the […]
