Update to Paste Backfill Design app

We have made a couple of changes to the Paste Backfill Design application since the original release. See the previous blog post for the main details of the app. Since the first release, we have modified the paste volume calculations to allow for multiple pouring locations and beach angles. This will be helpful for cases […]
Paste Backfill Design
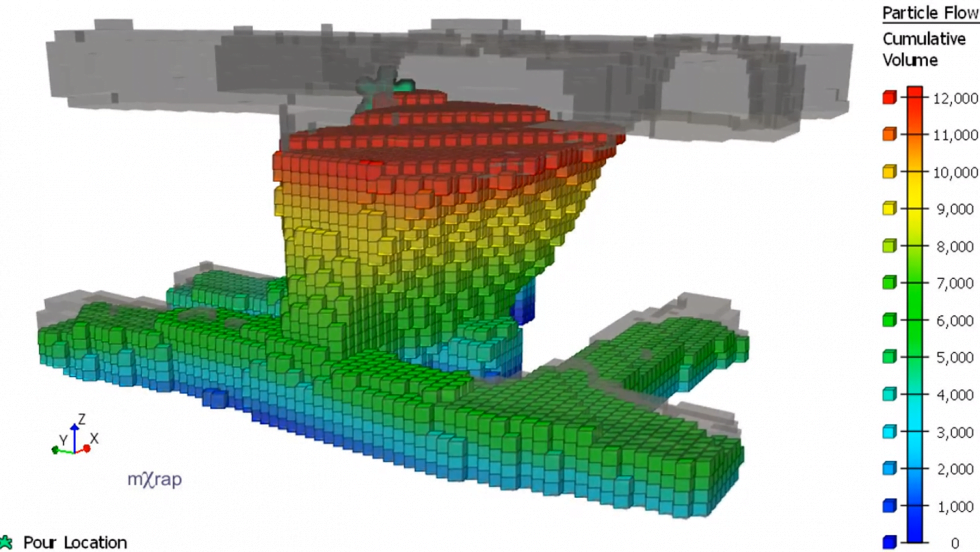
We have developed a new app to aid in the design of paste backfill in stoping operations. The app has tools to help you to: If you would like to try out the app, please contact our info email. Paste volumes The paste volume calculations use the mine geometry app to input surveyed geometry. Walls/barricades […]
