Yes, this is a frequently asked question…. MUL or MUpper-Limit refers to the truncating magnitude of the Gutenberg-Richter distribution. We used to refer to this as Mmax in the Hazard Assessment app and on the frequency-magnitude chart but we found there was confusion caused by Mmax being used to describe multiple things. Hopefully if we refer to MUL or the upper-limit magnitude, this will clear up the terminology a little.
A quick review on the terminology that concerns the frequency-magnitude chart and the Gutenberg-Richter distribution:
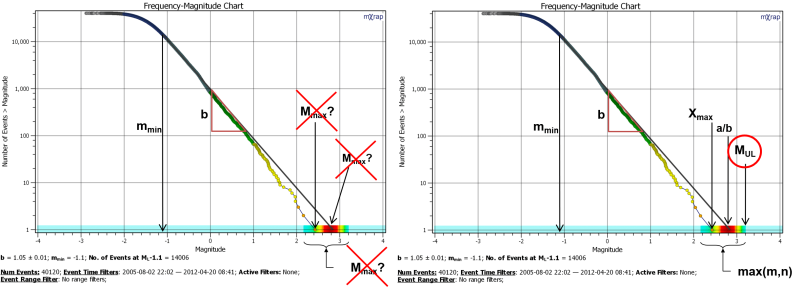
- Mmin – The magnitude of completeness, the dataset is considered complete above this magnitude (property of the data).
- b-value – The slope of the Gutenberg-Richter distribution, describes how the frequency of events scales with magnitude (property of the statistical model).
- Xmax – The largest magnitude event in the dataset (property of the data).
- a/b – The magnitude at N = 1 of the Gutenberg-Richter distribution (property of the model, maximum likelihood, see previous blog post).
- max(m,n) – This is the probability density function, given n events, of the largest event in that n events. This is a property of the Gutenberg-Richter statistical model. In other words, given a certain Gutenberg-Richter model, if you record N events, what is the largest event? This is not a single number but a likelihood distribution. The maximum likelihood of the largest event is the a/b value.
- MUL – The upper-limit magnitude of the max(m,n) distribution. It is an estimate only and a property of the statistical model.
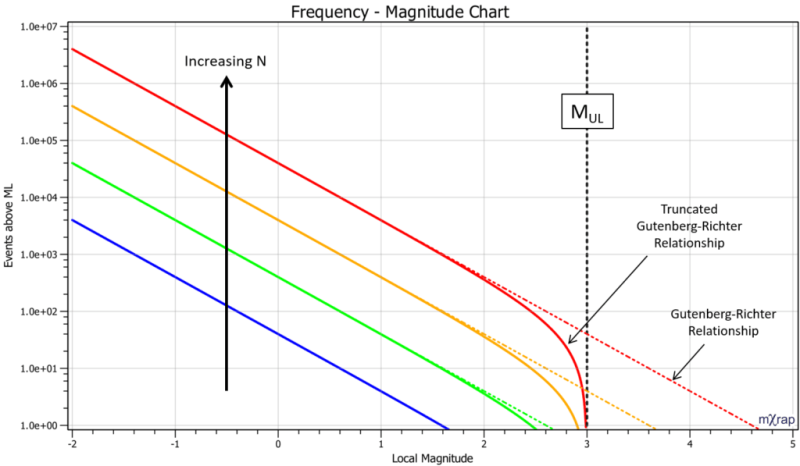
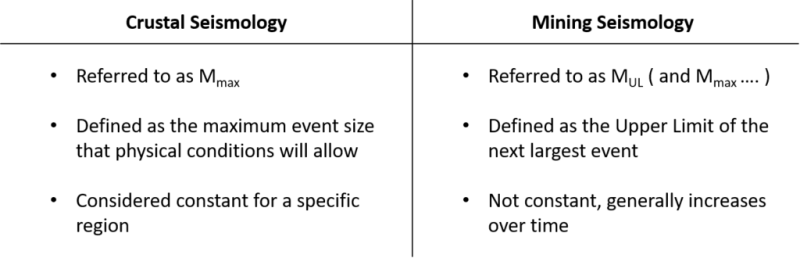
The truncating magnitude has slightly different meanings in mining seismology and crustal seismology. MUL is usually referred to as Mmax in crustal seismology literature and is generally considered constant for a particular area. In mining seismology MUL generally increases over time given the gradual increase in mining dimensions and loading of the rock mass. For this reason the definition is slightly modified in mining seismology to be the upper limit of the next largest event.
Why do we need an upper-limit or truncating magnitude?
The truncated Gutenberg-Richter distribution, rather than the open-ended distribution, is the most common frequency-magnitude relationship used in mine seismology. If there is no upper limit given to the Gutenberg-Richter distribution, then to evaluate the total energy of events in the relevant time period, the energy tends to infinity as the relationship is integrated above Mmin. This is clearly unrealistic.
We know there is a physical limit to possible magnitudes since the size of large earthquakes is related to the slip area of the fault and the physical size of faults is limited. Earthquakes on Earth above magnitude 10 (Richter) are essentially impossible given the size of known faults and a magnitude above 12 represents a fault area larger than the Earth itself!
So it is safe to say that MUL for a particular mine is going to be less than Richter Magnitude 10. The question is how much less is reasonable given the significantly reduced physical dimensions in mining.
How do we estimate MUL?
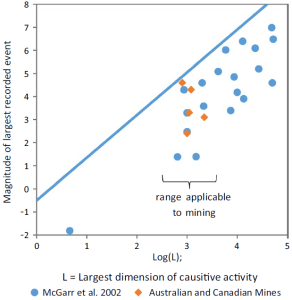
An empirical method of estimating MUL can be taken using a dataset compiled by McGarr et al. (2002) of large events and the largest dimension of the human activity associated with them. The figure on the right comes from Wesseloo (2018) who added a few extra points to the dataset from Australian and Canadian mines. The range applicable to mining indicates rough dimensions between 500 and 5,000m.
Aside from the empirical approach, there are also statistical approaches to estimating MUL. These generally take the form:
MUL ≈ Xmax + Δ
There are a number of different methods for calculating the Δ value. Many of these methods are described by Kijko and Singh (2011). Most of these have been implemented in the Hazard Assessment app along with the associated uncertainty of each method as described by Lasocki and Urban (2011).
It is better to over-estimate MUL than to under-estimate it. In terms of probabilistic seismic hazard calculations, the truncated Gutenberg-Richter model will always give a lower hazard result than the original Gutenberg-Richter, for magnitudes approaching MUL. For magnitudes well below MUL, the seismic hazard calculations are the same. In the Hazard Assessment app, we take the maximum of each MUL + σ estimate from multiple methods.
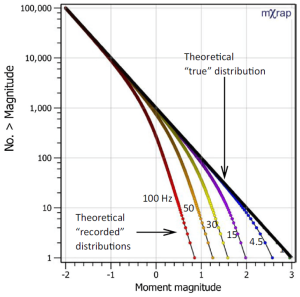
These statistical approaches assume the recorded magnitudes of large events are reliable. Moment is under-recorded for large events if there are no low-frequency sensors installed. The figure to the left comes from Morkel and Wesseloo (2017) showing the effect on the frequency-magnitude relationship, given certain sensor bandwidth limitations.
In cases like this it is best to override the MUL as it is likely to be under-estimated with statistical methods.
Conclusion
While it is important to understand what MUL is and how it effects seismic hazard calculations, it is not something to use for design purposes or to communicate seismic hazard. It is just one part of how seismic hazard is defined. By definition, the probability of an event exceeding MUL is zero, so it isn’t a great measure of seismic hazard.
If you have any questions regarding this topic, or something to add, feel free to leave a comment or send an email to support.
